ICAO Standard Atmosphere - ISA

Author:D.Thaler
Created:Aug 2013
Last changed:2019-08-11

Definitions and Equations

Definitions

The ICAO standard atmosphere (ISA) is defined within the meteorological scope as a reference atmosphere for mainly avionic purposes. The atmosphere is considered to be a dry ideal gas. The values of physical constants are shown in the following table:

Constants for the ICAO standard atmosphere
constant gravity \(g_0=\) 9.80665 m/s²
constant earth radius \(R=\) 6 356 766 m
molar mass of dry air \(M_d=\) 28.9644 kg/kmol
universal gas constant \(R_*=\) 8 314.32 J/(kmol K)
gas constant for dry air \(R_d=R_*/M_d \approx\) 287.053 J/(kg K)

ISA starts with surface values of temperature and pressure and continues with different levels of thermal stratification. Levels above 32 km are defined in ISA in 1993 but are neglected here.

h [km] T [C] \(\gamma\) [K/m] p [hPa]
0 +15.0 0.0065 1013.25
11 −56.5 0.0000  
20 −56.5 -0.0010  
32 −44.5    

Equations

Within this framework all necessary equations can be derived. Starting point is the hydrostatic approximation of the vertical component of the equation of motion, the so called hydrostatic equation:

(1)\[\frac{1}{\rho} \frac{\partial p}{\partial z} = -g_0\]

that states an equilibrium between vertical pressure gradient force per unit mass and gravity.

Inserting the ideal gas equation of dry air

(2)\[\rho = \frac{1}{ R_d} \frac{p}{T}\]

yields after some simple transformations

\[\frac{1}{p}\frac{\partial{p}}{\partial z} = \frac{\partial{\ln p}}{\partial z} = -\frac{g_0}{R_d}\frac{1}{T(z)} .\]

Integration between the limits \(h_0\) and \(h\) and exponentiation of the result gives the generalized barometric equation

(3)\[p = p_0 \exp\left( {-\frac{g_0}{R_d}\int_{h_0}^h{\frac{dz}{T(z)}}} \right )\]

with the pressure values \(p = p(h)\) and \(p_0 = p(h_0)\).

Isothermal Atmosphere

Given a vertically constant temperature \(T(z) = T_0\) the above equation simply gives

(4)\[p(h) = p_0 \exp \left[ -\frac{g_0 (h-h_0) }{R_d T_0} \right ]\]

The inverse function gives the geopotential height as function of the pressure difference for an isothermal atmosphere (a.k.a. hypsometric equation):

(5)\[\Delta h = (h - h_0) = - \frac{R_d T_0}{g_0} \ln\frac{p}{p_0}\]

that can be used for altimetry.

With the ideal gas equation a very similar expression can be derived for the density of air

(6)\[\rho(h) = \frac{p_0}{R_d T_0} \exp \left[ -\frac{g_0 (h-h_0) }{R_d T_0} \right ] = \rho_0 \exp \left[ -\frac{g_0 (h-h_0) }{R_d T_0} \right ] .\]

Vice versa the density altitude can be calculated as:

(7)\[\Delta h = (h - h_0) = - \frac{R_d T_0}{g_0} \ln \frac{\rho}{\rho_0} .\]

In ISA the isothermal equations are true for the “tropopause”-level between 11 km and 20 km altitude.

Politropic Atmosphere

From the surface up to 11 km and from 20 km to 32 km the temperature in ISA is not constant but shows a linear change with height:

(8)\[T(z) = T_0 - \gamma (z - h_0) = T_0 \left [ 1 - \gamma (z -h_0)/T_0 \right ] = T_0 \left [ 1 - \lambda (z - h_0) \right ]\]

( \(\lambda = \gamma / T_0\) ).

In equation (3) the integral must be solved between \(z = h_0\) and \(z = h\):

\[ \begin{align}\begin{aligned}\frac{1}{T_0} \int_{h_0}^h \frac{dz}{1 - \gamma (z - h_0)/T_0} =\\= \frac{1}{T_0} \int_0^{\Delta h} \frac{d(\Delta z)}{1 - \lambda \Delta z} =\\= -\frac{1}{T_0} \frac{1}{\lambda} \ln |1-\lambda z|\end{aligned}\end{align} \]

That finally gives for pressure as function of geopotential height:

(9)\[p(h) = p_0 \left [ 1 - \frac{\gamma}{T_0} (h - h_0) \right]^{g_0/(\gamma R_d)}\]

Solving the above equation for \(h\) gives the hypsometric equation for the polytropic atmosphere:

(10)\[h(p) - h_0 = \frac{T_0}{\gamma}\left[ 1 - \left (\frac{p}{p_0} \right )^{R_d \gamma / g_0} \right ]\]

Density as a function of height can easily be derived by the ideal gas equation \(\rho(h) = p(h)/(R_d T(h))\):

(11)\[\rho(h) = \underbrace{\frac{1}{R_d}\frac{p_0}{T_0}}_{\rho_0} \left[ 1 - \frac{\gamma}{T_0} (h - h_0) \right] ^ {\left [ g_0/(R_d \gamma) - 1\right ] }\]

Inverting the equation gives a relation between height and density (density altitude) for the polytropic atmosphere:

(12)\[h(p) - h_0 = \frac{T_0}{\gamma} \left [ 1 - \left( \frac{\rho}{\rho_0} \right)^\beta \right ]\]

with \(\beta = \left[g_0/(R_d\gamma) -1\right]^{-1}\)

Results

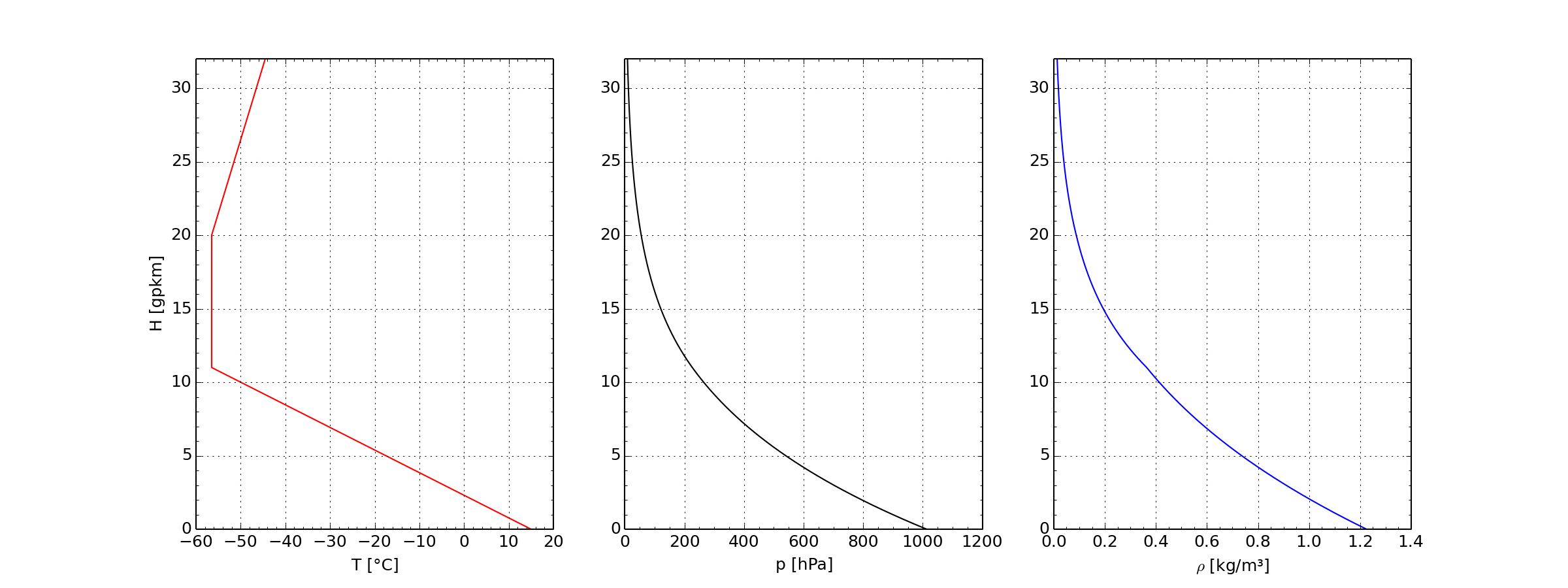
ICAO Standard Atmosphere up to 32 km height

ICAO standard atmosphere up to 32 km height

Left: Temperature in Celsius, Center: Pressure in Hektopascal,
Right: Density in Kilogram per Cubic Meter

The graphic was produced with the help of the Python program isaplots.py which also serves as demo program for the use of the Python library adisalib (for download in https://python3.foehnwall.at/adisalib.html or https://python2.foehnwall.at/adisalib.html ).

A table with an appropriate selection of values can be seen here:

h[gpm] T[C] p[hPa] \(\rho\) [kg/m³]
-300 16.95 1049.81 1.2608
0 15.00 1013.25 1.2251
500 11.75 954.60 1.1673
1000 8.50 898.74 1.1117
1500 5.25 845.55 1.0581
2000 2.00 794.94 1.0065
2500 -1.25 746.81 0.9569
3000 -4.50 701.07 0.9092
4000 -11.00 616.38 0.8192
5000 -17.50 540.18 0.7361
6000 -24.00 471.79 0.6597
7000 -30.50 410.58 0.5895
8000 -37.00 355.97 0.5252
9000 -43.50 307.40 0.4663
10000 -50.00 264.34 0.4127
11000 -56.50 226.30 0.3639
12000 -56.50 193.28 0.3108
14000 -56.50 141.00 0.2267
16000 -56.50 102.86 0.1654
18000 -56.50 75.03 0.1207
20000 -56.50 54.74 0.0880
24000 -52.50 29.30 0.0463
26000 -50.50 21.53 0.0337
28000 -48.50 15.86 0.0246
30000 -46.50 11.72 0.0180
32000 -44.50 8.68 0.0132

Table of symbols

\(h\) geopotential height [gpm]
\(p\) pressure [Pa]
\(T\) Temperature [K]
\(z\) geopotential height [gpm]
\(\gamma\) vertical temperature gradient \((-\partial T/\partial z)\) [K/m]
\(\rho\) air density [kg/m³]

References

Any comments to info at foehnwall dot at