Multiple scattering of short wave radiation between ground and atmosphere¶
A rough estimate
| Author: | D.Thaler |
|---|---|
| Created: | Aug 2015 |
| Last changed: | 2018-05-01 |
Note
Broadband radiation is considered, meaning a convolution in the form
is used. \(V(\lambda)\) being e.g. the Luminous efficacy or any other spectral filter function.
Symbols
- \(I_0\) … incomming short wave radiation flux per area above the clouds (incomming irradiance)
- \(I_{art}\) … outgoing ground based short wave radiation flux per unit area (“artificial” radiation flux)
- \(S\) … resulting areal mean of the incomming short wave radiation flux at the ground (ground irradiance)
- \(B\) … scatterd radiation from the ground to the atmosphere
- \(N\) … fraction of cloud cover between 0 (sky clear) and 1 (overcast)
- \(A_{t}\) … albedo of the cloud tops
- \(A_{b}\) … albedo of the cloud bottom
- \(A_{g}\) … albedo of the ground
- \(d_{t}\) … upward backscattering albedo of the clear atmosphere
- \(d_{b}\) … downward backscattering albedo of the celar atmosphere
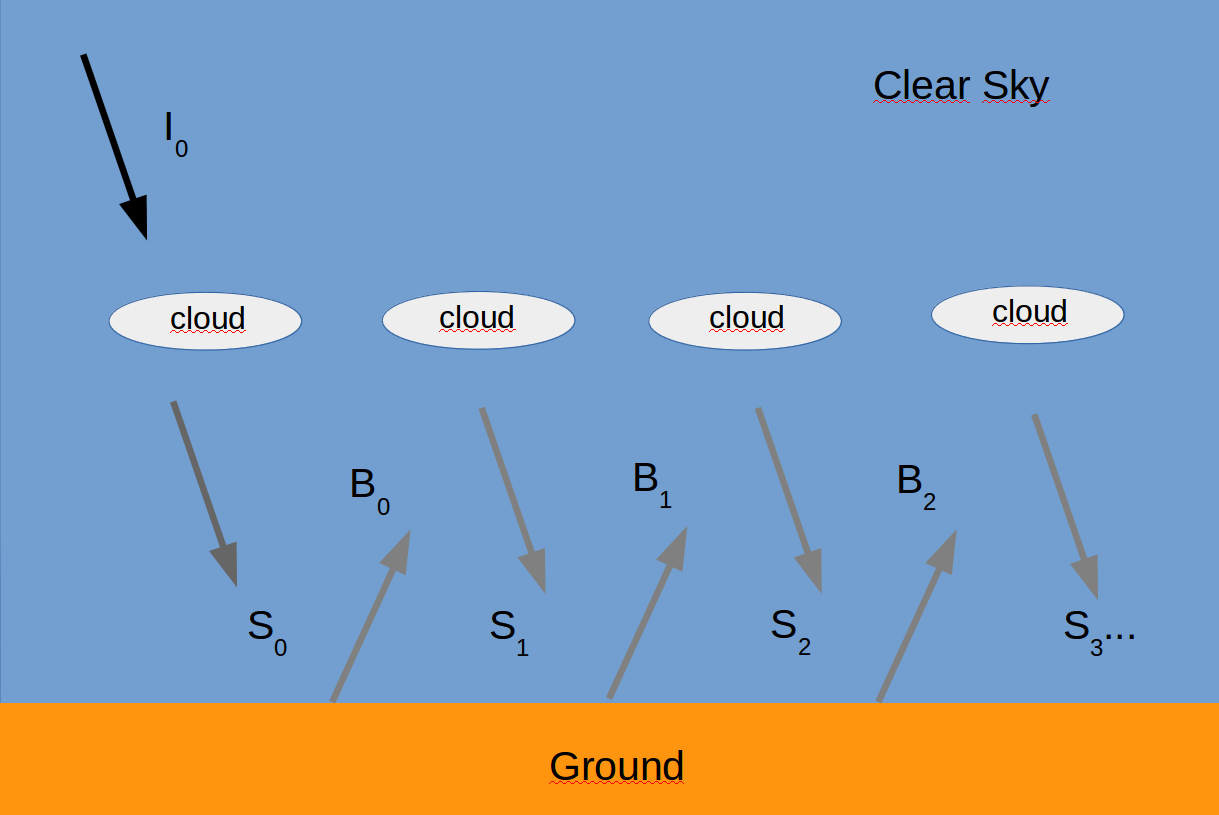
Multiple scattering between ground and clouds¶
Incomming short wave radiation is scattered by a layer of clouds. A part reaches the ground, a part of it is scatterd back to the clouds, a part of it is again back scatterd to the ground, and so on …
Note
- Back scattering effects in the clear sky are neglected.
- Absorption is neglected at all
- Areal mean fluxes are calculated, so e.g. the abnormal high radiation with the sun shining thru a spot in an almost closed cloud cover is not considerated.
Calculation¶
Wanted \(S = S(I_0, N, A_t, A_b, A_g)\).
Radiation from above:
\[I_0\]Radiation scatterd uppwards from the clouds:
\[I_0 N A_t\]Radiation below the clouds comming from above:
\[S_0 = I_0 \left[ (1-N) + N (1-A_t) \right] = I_0 \left[ 1-N + N - A N_t \right] = I_0 \left[ 1 - N A_t \right]\]Fraction of the radiation below the clouds scatterd back upwards by the ground:
\[B_0 = S_0 A_g = I_0 (1-N A_t) A_g\]The fraction of \(B_0\) that is scatterd down again:
\[S_1 = B_0 A_b N = I_0 (1- N A_t) A_g A_b N\]Up and down of the scattered radiation gives the next term:
\[S_2 = B_1 A_n N = S_1 A_g A_b N = I_0 (1- N A_t) (A_g A_b N) (A_g A_b N) = I_0 (1- N A_t) (A_g A_b N)^2\]Continuing one yields an infnite series:
\[S = I_0 (1 - N A_t) \sum_{k=0}^{\infty} (A_g A_b N)^k\]\(0 \leq A_g A_b N \lt 1\) in the series above is converging and yields the geometric series \(1 + x + x^2 + x^3 + ... = 1/(1-x)\) Therefore we get the
Ground irradiance dependent on ground and cloud scattering
The above derivation follows largely Nielsson (2007) except for Nielssons conjecture of summing downgoing irradiance \(S\) and upgoing math:B to get the total irradiance (or illuminace) for the scenery.
Multiple scattering between ground and clear atmosphere¶
Incomming short wave radiation is scattered only by the atmosphere. A part of it reaches the ground, a part of it is scatterd back to the atmosphere, a part of it is again back scatterd to the ground, and so on …
Note
- No clouds
- Absorption is neglected at all
- Areal mean fluxes are calculated, so e.g. the abnormal high radiation with the sun shining thru a spot in an almost closed cloud cover is not considerated.
Calculation¶
Wanted \(S = S(I_0, N, d_t, d_b)\).
Radiation from above:
\[I_0\]Radiation backscatterd (uppwards) from atmosphere to sky:
\[I_0 d_t\]Direct radiation reaching the ground:
\[S_0 = I_0 (1-d_t)\]Fraction of \(S_0\) scatterd back upwards by the ground:
\[B_0 = S_0 A_g = I_0 (1-d_t) A_g\]The fraction of \(B_0\) that is scatterd down again:
\[S_1 = B_0 d_b = I_0 (1- d_t) A_g d_b = S_0 (A_g d_b)\]Up and down of the scattered radiation gives the next term:
\[ \begin{align}\begin{aligned}B_1 = S_1 A_g\\S_2 = B_1 d_b = S_1 (A_g d_b) = S_0 (A_g d_b)^2 = I_0 (1-d_t) (A_g d_b)^2\end{aligned}\end{align} \]Continuing one yields an infnite series:
\[S = I_0 (1 - d_t) \sum_{k=0}^{\infty} (A_g d_b)^k\]\(0 \leq A_g d_b \lt 1\) in the series above is converging and yields the geometric series \(1 + x + x^2 + x^3 + ... = 1/(1-x)\) Therefore we get the
Ground irradiance dependent on ground and clear atmosphere scattering
Multiple scattering between ground, clear atmosphere AND CLOUDS¶
Incomming short wave radiation is scattered only by the atmosphere. A part of it reaches the ground, a part of it is scatterd back to the atmosphere, a part of it is again back scatterd to the ground, and so on …
Note
- Absorption is neglected at all
- Areal mean fluxes are calculated, so e.g. the abnormal high radiation with the sun shining thru a spot in an almost closed cloud cover is not considerated.
- Atmospheric backscattering is only considered to be active on the clear sky portion of the radiation and not on the part of the radiation scattered by clouds [maybe arguable!]
Calculation¶
Wanted \(S = S(I_0, N, d_t, d_b)\).
Radiation from above:
\[I_0\]Radiation backscatterd (uppwards) from atmosphere to sky:
\[I_0 \left [ (1-N)d_t + N A_t \right ] = I_0 \left [ d_t + N(A_t - d_t) \right ]\]Direct radiation reaching the ground:
\[S_0 = I_0 \left [ 1 - d_t - N(A_t - d_t) \right ]\]Fraction of \(S_0\) scatterd back upwards by the ground:
\[B_0 = S_0 A_g = I_0 \left [ 1 - d_t - N(A_t - d_t) \right ] A_g\]The fraction of \(B_0\) that is scatterd down again:
\[S_1 = B_0 \left [ N A_b + (1-N) d_b \right ] = S_0 \left [ N A_b + (1-N) d_b \right ] A_g\]Up and down of the scattered radiation gives the next term:
\[ \begin{align}\begin{aligned}B_1 = S_1 A_g\\S_2 = B_1 \left [ N A_b + (1-N) d_b \right ] = S_1 \left [ N A_b + (1-N) d_b \right ] A_g\\S_2 = S_0 \left [ N A_b + (1-N) d_b \right ]^2 A_g^2\\S_2 = I_0 \left [ 1 - d_t - N(A_t - d_t) \right ] \left [ N A_b + (1-N) d_b \right ]^2 A_g^2\end{aligned}\end{align} \]Continuing the procedure yields an infnite series:
\[S = I_0 \left [ 1 - d_t - N(A_t - d_t) \right ] \sum_{k=0}^{\infty} \underbrace{\left [ N A_b A_g+ (1-N) d_b A_g \right ]^k}_{x^k}\]Because of \(0 \lt x \leq 1\) the series above is converging and yields the geometric series \(1 + x + x^2 + x^3 + ... = 1/(1-x)\) Therefore we get after some simple arithmetic the
Ground irradiance dependent on ground, cloud and clear atmosphere scattering comming from radiation from above
Special cases¶
No clouds: Setting in equation (3) \(N=0\), we get:
\[\frac{S}{I_0} = \frac{ (1 - d_t) - 0 (A_t - d_t)}{(1- A_g d_b) - 0 A_g (A_b - d_b)} = \frac{ (1 - d_t)}{(1- A_g d_b)}\]that resembles equation (2).
Overcast with clouds: (added at 2017-02-21): Setting in equation (3) \(N=1\), we get:
(4)¶\[\frac{S}{I_0} = \frac{ (1 - d_t) - 1 (A_t - d_t)}{(1- A_g d_b) - 1 A_g (A_b - d_b)} = \frac{ (1 - A_t)}{(1- A_g A_b)}\]Meaning that overcast sky does not show any influence by clear sky (purely atmospheric) scattering. This approach might be arguable.
No scattering in the clear atmosphere: Setting Setting in equation (3) \(d_t = d_b =0\), we get:
\[\frac{S}{I_0} = \frac{ (1 - 0) - N (A_t - 0)}{(1- A_g 0) - N A_g (A_b - 0)} = \frac{1 - N A_t}{ 1 - N A_g A_b}\]that resembles equation (1).
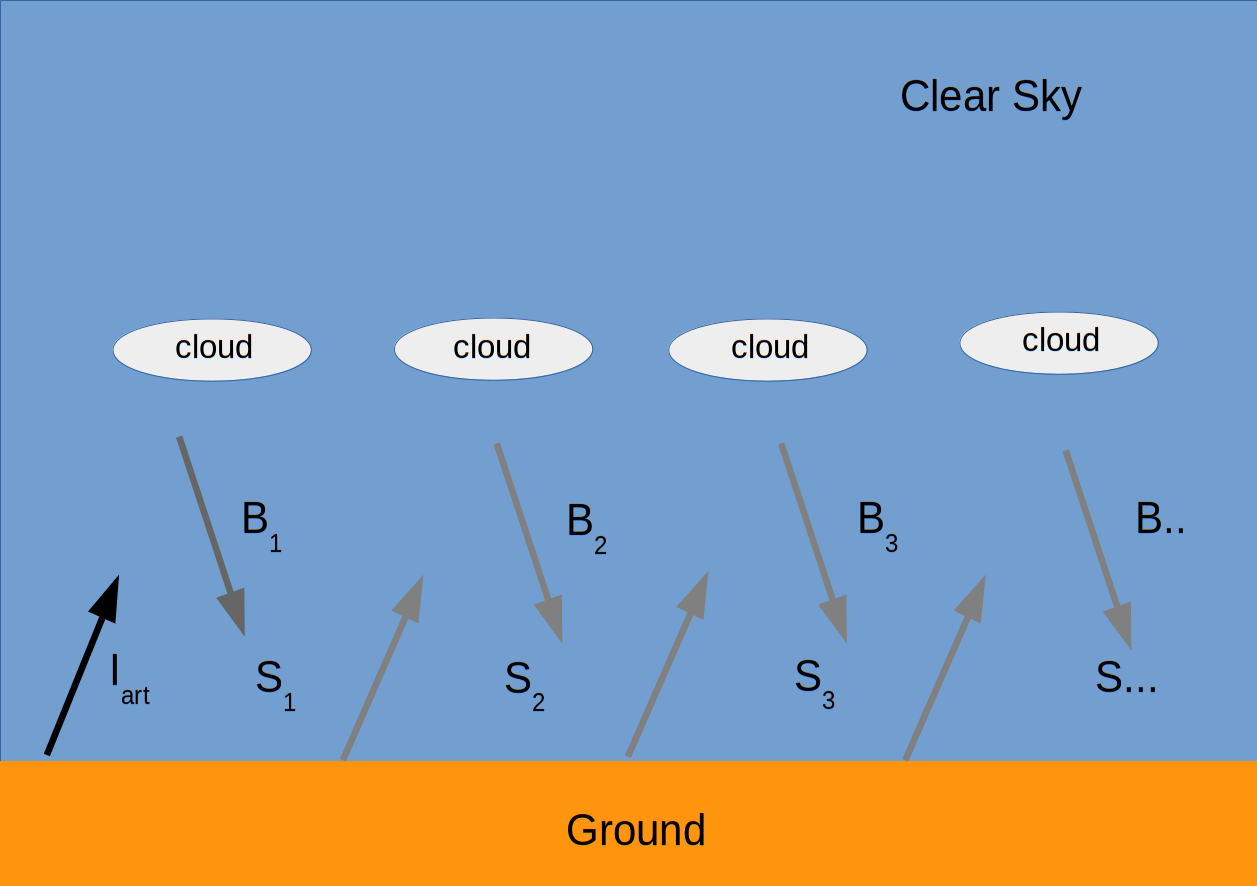
Multiple scattering of outgoing ground based radiation¶
Now let’s assume we have broad band radiation emitted diffusely from the ground from e.g. artificial sources \(I_{art}\) upward towards the sky.
upgoing \(I_{art}\) is scattered down by a layer of clouds and by the clear sky (where there are no clouds) because of Raleigh and Mie scattering at molecules and particles:
This downward radiation flux is diffusly reflected by the ground
and then again reflected by clouds and clear atmosphere towards the ground:
and so forth.
The \(k-\) th order downward flux reads
Summing up the infinitite series
results in (with help of the relation for binomical or geometric series
and finally in:
Ground irradiance because of ground based artificial illumination including multiple scattering by clouds, atmosphere and ground
Albedo values¶
Rough estimates derived form Möller (1965) and Nielsson (2007). Any dependence of the direction of the incoming radiation is neglected.
| Remark | Value |
|---|---|
| Cloud top \(A_t\) | |
| NS | 0.90 |
| SC | 0.70 |
| ST or thin SC | 0.65 |
| Cloud bottom \(A_b\) | |
| NS | 0.90 |
| SC | 0.70 |
| ST | 0.65 |
| thin ST or SC | 0.50 |
| thick AC or AS | 0.70 |
| CS | 0.35 |
| CI (or haze) | 0.20 |
| Ground \(A_g\) | |
| sea without waves | 0.20 |
| sea with moderate to high waves | 0.04 |
| ice without snow | 0.55 |
| ice with fresh snow | 0.80 |
| dense forest, no snow | 0.05 |
| dense forest, dry snow | 0.50 |
| wet ground | 0.05 |
| humid ground | 0.10 |
| dry ground | 0.20 |
| snow slush | 0.35 |
| dry fresh snow | 0.70 |
| old snow, half covering | 0.25 |
| desert | 0.25 |
| Atmospheric albedo \(d=d_t=d_b\) | (Möller, 1965) |
| Rayleigh atmosphere | 0.07 |
| medium turbid atmosphere | 0.15 |
| highly turbid atmosphere | 0.25 |
Alternatively a reasonably good internet source can be found here:
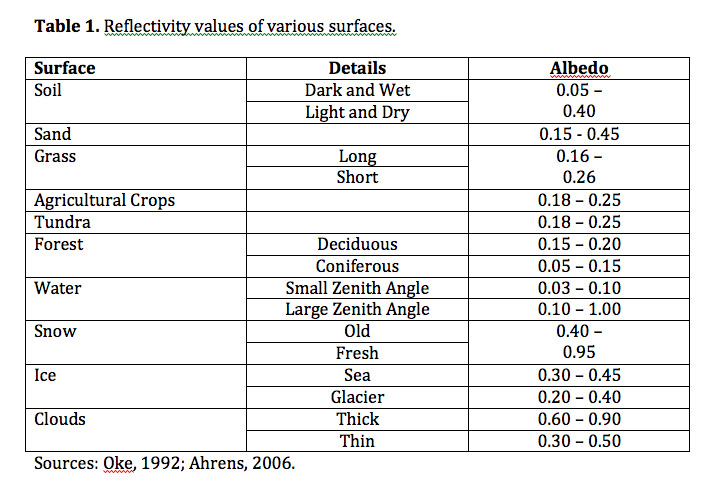
From The Encyclopedia of Earth - Albedo (Creative Commons Attribution-Share Alike license.), retrieved Aug 2015.
References¶
- Craig. F. Bohren, Eugene E. Clothiaux (2006): Fundamentals of Atmospheric Radiation: An Introduction with 400 Problems. 490 pages. Wiley-VCH. Weinheim/Germany. p. 241 ff. “Multiple Scattering”
- Fritz Möller: On the backscattering of global radiation by the sky. Tellus XVII (1965), 3 (Retrieved Aug. 2015)
- Lena Nilsson: Hur mörkt blir det? Institutionen för geovetenskaper, Uppsala Universitet, Juni 2007. (Retrieved Oct. 2014). Available as an internal German translation.