Some pressure reduction methods

Author:D.Thaler
Created:Aug 2019
Last changed:2019-08-15

Reducing the pressure measurment of some place to sea level looks to be an easy task. But several assumptions have to be made about:

  1. the virtuell stratification of temperature and humidity
  2. the structure of the gravity field

More or less sophisticated methodes have been developed. Here we simply follow the description of the basic equations and how the recommended methods of WMO and ICAO are related to that.

Basic equations

Assuming there is no vertically accelerated windfield the vertical component of the atmospheric equation of motion degenerates to the hydrostatic equation \(\frac{1}{\rho} \frac{\partial p}{\partial z} = -g\). Basic transformations with the help of the ideal gas equation \(\rho = \frac{1}{ R_d} \frac{p}{T}\) gives the general integrated form between the limits \(h_0\) and \(h\):

(1)\[p = p_0 \exp\left( {-\int_{h_0}^h{\frac{g}{R_d T(z)}} dz} \right ) = p_0 \exp\left( {-\frac{g_0}{R_d}\int_{h_0}^h{\frac{dz}{T(z)}} } \right ).\]

The outermost right expression is valid with the assumption both \(g\) and \(R_D\) are independent of the geometric height. Because of the fundamental theorem of calculus there is an equivalent formulation:

(2)\[p(h) = p_0 \exp \left[ -\frac{g_0}{R_d} \frac{(h-h_0) }{\overline{T}}\right ]\]

The barometric mean Temperature \(\overline{T}\) is defined by the integral

(3)\[\frac{1}{\overline{T}} = \frac{1}{h-h_0}\int_{h_0}^{h}\frac{dz}{T(z)}\]

All relations above apply to a dry atmosphere. In humid air with variable water vapor content the gas constant should be modified. Instead of working with variable gas constants it’s more practicable to define a temperature with all the necessary changes packed into, the Virtual Temperature:

(4)\[\begin{split}T_v = (1+C\,q)T \\ C = (R_v/R_d -1) \approx 0.61\end{split}\]

\(q=\rho_v/\rho\) is the specific humidity, the ratio of the density of water vapor to the density of humid air.

Isothermal Atmosphere

Given a vertically constant temperature \(T(z) = \overline{T} = T_0\) the above equation simplifies to:

(5)\[p(h) = p_0 \exp \left[ -\frac{g_0 (h-h_0) }{R_d T_0} \right ]\]

The inverse function gives the geopotential height as function of the pressure difference for an isothermal atmosphere (a.k.a. hypsometric equation):

(6)\[\Delta h = (h - h_0) = - \frac{R_d T_0}{g_0} \ln\frac{p}{p_0}\]

that can be used for altimetry.

Politropic Atmosphere

A sometimes better approach is the assumption of a linear temperature profile:

(7)\[T(z) = T_0 - \gamma (z - h_0) = T_0 \left [ 1 - \frac{\gamma}{T_0} (z - h_0) \right ].\]

Doing the integration yields the solution for pressure as function of the geopotential height:

(8)\[p(h) = p_0 \left [\frac{T(z)}{T_0} \right ]^{g_0/(\gamma R_d)} = p_0 \left [ 1 - \frac{\gamma}{T_0} (h - h_0) \right]^{g_0/(\gamma R_d)}\]

Solving the above equation for \(h\) gives the hypsometric equation for the polytropic atmosphere:

(9)\[h(p) - h_0 = \frac{T_0}{\gamma}\left[ 1 - \left (\frac{p}{p_0} \right )^{R_d \gamma / g_0} \right ]\]

Density as a function of height can easily be derived by the ideal gas equation \(\rho(h) = p(h)/(R_d T(h))\):

(10)\[\rho(h) = \underbrace{\frac{1}{R_d}\frac{p_0}{T_0}}_{\rho_0} \left[ 1 - \frac{\gamma}{T_0} (h - h_0) \right] ^ {\left [ g_0/(R_d \gamma) - 1\right ] }\]

Results

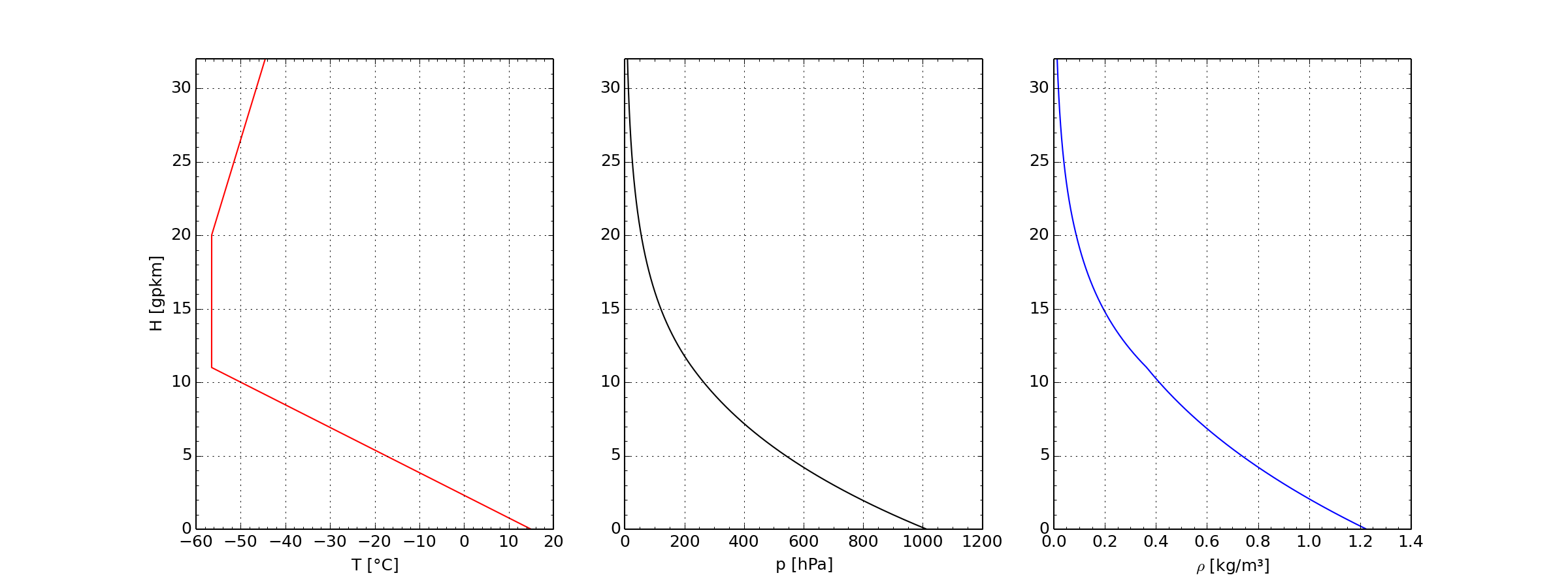
ICAO Standard Atmosphere up to 32 km height

ICAO standard atmosphere up to 32 km height

Left: Temperature in Celsius, Center: Pressure in Hektopascal,
Right: Density in Kilogram per Cubic Meter

A table with an appropriate selection of values can be seen here:

h[gpm] T[C] p[hPa] \(\rho\) [kg/m³]
-300 16.95 1049.81 1.2608
0 15.00 1013.25 1.2251
500 11.75 954.60 1.1673
1000 8.50 898.74 1.1117
1500 5.25 845.55 1.0581
2000 2.00 794.94 1.0065
2500 -1.25 746.81 0.9569
3000 -4.50 701.07 0.9092
4000 -11.00 616.38 0.8192
5000 -17.50 540.18 0.7361
6000 -24.00 471.79 0.6597
7000 -30.50 410.58 0.5895
8000 -37.00 355.97 0.5252
9000 -43.50 307.40 0.4663
10000 -50.00 264.34 0.4127
11000 -56.50 226.30 0.3639
12000 -56.50 193.28 0.3108
14000 -56.50 141.00 0.2267
16000 -56.50 102.86 0.1654
18000 -56.50 75.03 0.1207
20000 -56.50 54.74 0.0880
24000 -52.50 29.30 0.0463
26000 -50.50 21.53 0.0337
28000 -48.50 15.86 0.0246
30000 -46.50 11.72 0.0180
32000 -44.50 8.68 0.0132

Table of symbols

\(h\) geopotential height [gpm]
\(p\) pressure [Pa]
\(T\) Temperature [K]
\(z\) geopotential height [gpm]
\(\gamma\) vertical temperature gradient \((-\partial T/\partial z)\) [K/m]
\(\rho\) air density [kg/m³]

Definitions

The ICAO standard atmosphere (ISA) is defined within the meteorological scope as a reference atmosphere for mainly avionic purposes. The atmosphere is considered to be a dry ideal gas. The values of physical constants are shown in the following table:

Constants for the ICAO standard atmosphere
constant gravity \(g_0=\) 9.80665 m/s²
constant earth radius \(R=\) 6 356 766 m
molar mass of dry air \(M_d=\) 28.9644 kg/kmol
universal gas constant \(R_*=\) 8 314.32 J/(kmol K)
gas constant for dry air \(R_d=R_*/M_d \approx\) 287.053 J/(kg K)

ISA starts with surface values of temperature and pressure and continues with different levels of thermal stratification. Levels above 32 km are defined in ISA in 1993 but are neglected here.

h [km] T [C] \(\gamma\) [K/m] p [hPa]
0 +15.0 0.0065 1013.25
11 −56.5 0.0000  
20 −56.5 -0.0010  
32 −44.5    

References

Any comments to info at foehnwall dot at